domingo, 11 de outubro de 2015
Estudo do sinal da função quadrática
Considere a função quadrática ax² + bx + c ( a b e c reais com a diferente de 0 ) são estudados por meio de análises do coeficiente a e de delta .
Quando f(x) > 0, f(x) = 0 ou f(x) < 0
1° iguala a função a zero, e calcule-se as raízes ou zeros da função
2° marca na reta numérica as raízes encontradas
3° fora das raízes tem o mesmo sinal do coeficiente de a. E dentro, isto é, entre as raízes a função terá sinal contrario ao coeficiente de a .
Quando f(x) > 0, f(x) = 0 ou f(x) < 0
1° iguala a função a zero, e calcule-se as raízes ou zeros da função
2° marca na reta numérica as raízes encontradas
3° fora das raízes tem o mesmo sinal do coeficiente de a. E dentro, isto é, entre as raízes a função terá sinal contrario ao coeficiente de a .
Estudo dos sinais:
++++ + - - - - - - + + + +
3 4
Se x<3 ou="" x="">4, então f(x)>0
se 3 < x < 4, então f(x) <0 span="">
se x=3 ou x=4, então f(x)=0
Estudo dos sinais:
- - - - - - + + + + + + - - - - - - -
-1 6
f(x)=0 para x = -1 ou x = 6
f(x) > 0 para x < -1 ou x > 6
f(x) < 0 para -1 < x < 4
- Estudo dos sinais:
+ + + + + + . + + + + + +
2
f(x)=0 para x = 2
f(x)>; 0 para x diferente de 2
f(x) nunca será negativa
sábado, 10 de outubro de 2015
EXERCÍCIOS DE RADICIAÇÃO COM RESPOSTAS
Escreva simplificadamente:: A)  B)  C)  Racionalize os denominadores: A)  B)  C)  D)  E)  RESPOSTAS 1º
Resposta a:
Resposta b:
Resposta c:
 RESPOSTAS 2º
Resposta A:
Resposta B:
Resposta C:
Resposta D:
Resposta F:
 |
Radiciação de números complexos
Seja o número complexo z = r (cosq + i . senq ).
Para o cálculo das raízes e-nésimas do complexo z, ou seja, para o cálculo de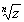
, deveremos utilizar a seguinte fórmula:
Para o cálculo das raízes e-nésimas do complexo z, ou seja, para o cálculo de
, deveremos utilizar a seguinte fórmula:
onde k = 0,1,2,3, ... , n - 1.
Esta fórmula é aparentemente assustadora, não é?!
Vamos então, por partes.
1 - O ângulo q (argumento do complexo) deve ser expresso em graus. Se você preferir usar a unidade radiano, ao invés de 360.k, deverá ser usado 2kp , pois 360 graus = 2p radianos.
2 - Como k = 0,1,2,.3, ... , n -1, então são n valores possíveis para a variável k, o que significa que existem n raízes e-nésimas de z. Ou seja: 2 raízes quadradas, três raízes cúbicas, quatro raízes quartas, cinco raízes quintas, etc.
3 - Observe que todas as n raízes e-nésimas de z possuem o mesmo módulo.
Vamos determinar, como exemplo, as três raízes cúbicas da unidade.
Esta fórmula é aparentemente assustadora, não é?!
Vamos então, por partes.
1 - O ângulo q (argumento do complexo) deve ser expresso em graus. Se você preferir usar a unidade radiano, ao invés de 360.k, deverá ser usado 2kp , pois 360 graus = 2p radianos.
2 - Como k = 0,1,2,.3, ... , n -1, então são n valores possíveis para a variável k, o que significa que existem n raízes e-nésimas de z. Ou seja: 2 raízes quadradas, três raízes cúbicas, quatro raízes quartas, cinco raízes quintas, etc.
3 - Observe que todas as n raízes e-nésimas de z possuem o mesmo módulo.
Vamos determinar, como exemplo, as três raízes cúbicas da unidade.
Seja o número complexo z = 1 (unidade).
Podemos escrever na forma polar: z = 1 (cos 0º + i . sen 0º)
Temos então:
módulo: r = 1
argumento: q = 0º = 0 rad
Substituindo na fórmula dada, vem:
Podemos escrever na forma polar: z = 1 (cos 0º + i . sen 0º)
Temos então:
módulo: r = 1
argumento: q = 0º = 0 rad
Substituindo na fórmula dada, vem:
Fazendo k = 0, obteremos a primeira raiz, ou seja:
z1 = 1(cos 0º + i . sen 0º) = 1(1 + i . 0) = 1Fazendo k = 1, obteremos a segunda raiz, ou seja:
z2 = 1(cos 120º + i . sen 120º) = -1/2 + i . Ö 3 / 2
z1 = 1(cos 0º + i . sen 0º) = 1(1 + i . 0) = 1Fazendo k = 1, obteremos a segunda raiz, ou seja:
z2 = 1(cos 120º + i . sen 120º) = -1/2 + i . Ö 3 / 2
Finalmente, fazendo k = 2, obteremos a terceira e última raiz:
z3 = 1(cos 240º + i . sen 240º) = -1 /2 - i . Ö 3 / 2
z3 = 1(cos 240º + i . sen 240º) = -1 /2 - i . Ö 3 / 2
Um detalhe importante pode ser visualizado no exemplo acima: os argumentos das raízes são 0º, 120º e 240º , que são termos de uma progressão aritmética de razão 120º. Isto não é uma coincidência! Veja a dica abaixo:
As n raízes enésimas de um número complexo de argumento q , possuem argumentos que formam uma
Progressão Aritmética de primeiro termo q / n e razão 360º / n.
Progressão Aritmética de primeiro termo q / n e razão 360º / n.
Sabendo disto, poderemos simplificar o cálculo das raízes de um número complexo.Por exemplo, vamos calcular as raízes quadradas da unidade imaginária:
Temos z = i ( i = unidade imaginária).
Portanto, z = 1(cos 90º + i . sen 90º)
módulo: r = 1
argumento: q = 90º
Como queremos as raízes quadradas, temos n = 2. Pela dica acima, os argumentos das raízes formarão uma P. A . de primeiro termo 90º / 2 = 45º e razão igual a 360 / n = 360 / 2 = 180º. Logo, basta determinar a primeira raiz e usar esta informação para calcular a segunda e última raiz.
Portanto, z = 1(cos 90º + i . sen 90º)
módulo: r = 1
argumento: q = 90º
Como queremos as raízes quadradas, temos n = 2. Pela dica acima, os argumentos das raízes formarão uma P. A . de primeiro termo 90º / 2 = 45º e razão igual a 360 / n = 360 / 2 = 180º. Logo, basta determinar a primeira raiz e usar esta informação para calcular a segunda e última raiz.
Temos:
1ª raiz: fazendo k = 0, vem z1 = 1(cos 45º + i . sen 45º) = Ö 2 / 2 + i . Ö 2 / 2
2ª raiz: z2 = 1(cos 225º + i . sen 225º) = - Ö 2 /2 - i .Ö 2 / 2
Observe que 225º = 45º + 180º (180º = 360 / n = 360 / 2 (veja acima).
2ª raiz: z2 = 1(cos 225º + i . sen 225º) = - Ö 2 /2 - i .Ö 2 / 2
Observe que 225º = 45º + 180º (180º = 360 / n = 360 / 2 (veja acima).
Mais um exercício resolvido para você!
Resolva a equação z6 - 16z3 + 64 = 0 , onde z Î C (C = conj. dos números complexos).
Vamos começar fazendo z3 = x ; Daí, vem z6 = (z3)2 = x2 ; substituindo, fica:
x2 - 16x + 64 = 0 \ (x - 8)2 = 0 \ x = 8
Como z3 = x , vem z3 = 8 . O problema consiste então no cálculo das raízes cúbicas de 8. Observe
que 8 = 8 + 0. i ( i = unidade imaginária).
Resolva a equação z6 - 16z3 + 64 = 0 , onde z Î C (C = conj. dos números complexos).
Vamos começar fazendo z3 = x ; Daí, vem z6 = (z3)2 = x2 ; substituindo, fica:
x2 - 16x + 64 = 0 \ (x - 8)2 = 0 \ x = 8
Como z3 = x , vem z3 = 8 . O problema consiste então no cálculo das raízes cúbicas de 8. Observe
que 8 = 8 + 0. i ( i = unidade imaginária).
Portanto:
Sabemos que existem três raízes cúbicas; logo, fazendo k = 0, obteremos a primeira raiz:
z1 = 2(cos 0º + i . sen 0º) = 2(1 + 0.i) = 2
Usando a dica vista acima , vem:
z2 = 2(cos 120º + i. sen 120º) = 2(- 1 /2 + i . Ö 3 / 2) = - 1 + Ö 3 i
z3 = 2(cos 240º + i . sen 240º) = 2[- 1 /2 + i . (- Ö 3 / 2) = -1 - Ö 3 i
z1 = 2(cos 0º + i . sen 0º) = 2(1 + 0.i) = 2
Usando a dica vista acima , vem:
z2 = 2(cos 120º + i. sen 120º) = 2(- 1 /2 + i . Ö 3 / 2) = - 1 + Ö 3 i
z3 = 2(cos 240º + i . sen 240º) = 2[- 1 /2 + i . (- Ö 3 / 2) = -1 - Ö 3 i
Portanto, o conjunto solução da equação dada é:
S = {2; -1 + Ö 3 i; -1 - Ö 3 i}
S = {2; -1 + Ö 3 i; -1 - Ö 3 i}
quinta-feira, 8 de outubro de 2015
EQUAÇÕES DE 2 GRAU E SUAS APLICAÇÕES
Na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão
Não se engane, mesmo sem perceber as equações do 2º grau e a função do 2° grau estão presentes em inúmeras situações cotidianas. É claro que nós não a usamos todos os dias ou em tudo. Você não acorda num belo domingo de manhã e tem que ao escovar os dentes resolver um delta ou calcular a raiz da equação para um sorriso perfeito. Mas que as aplicações existem existem.
Como exemplo temos que,
- Movimento de um projétil - Você já deve ter estado na beira de um rio ou de um lago e atirado uma pedra para o centro da água ou então jogado um objeto ou dado uma bicuda pro alto em uma bola. Note que como será a trajetória desse movimento? Uma parábola, a função do 2° grau que descreve este movimento. Olha uma equação do 2° grau ai gente !!!
Veja se a trajetória de um projétil, perceba o movimento descrito, uma parábola. A equação do segundo grau é forte presença ai. Por exemplo, para calcular a altura máxima atingida você presisa calcular o delta, para descobrir o ponto de partida e chegada é necessário resolver a equação e achar os valores de x.
Veja também quando é arremessado uma bola de canhão ou quando atira ao centro do lago se parece com a que aparece nas seguintes simulações, uma parábola.
- na Física ela possui um papel importante na análise dos movimentos uniformemente variados (MUV), pois em razão da aceleração, os corpos variam a velocidade e o espaço em função do tempo.
Na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão
S = S0 + V0t + (at2)/2, onde a: aceleração, S: espaço, V: velocidade e t: tempo.
Olhem só: Um móvel realiza um MUV obedecendo à função S = 2t2 - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido?
Olhem só: Um móvel realiza um MUV obedecendo à função S = 2t2 - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido?
Olha uma equação do 2° grau ai gente !!!
Resolução: A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel:
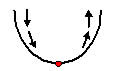
Resolução: A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel:
- Olha outra aplicação na física da equação do 2° grau a Lei da Queda dos Corpos
No estudo de física a queda livre é uma particularização do movimento uniformemente variado (MRUV). Um famoso físico e astrônomo italiano chamado Galileu Galilei, introduziu o método experimental e acreditava que qualquer afirmativa só poderia ser confirmada após a realização de experimentos e a sua comprovação. No seu experimento mais famoso ele, Galileu Galilei, estando na Torre de Pisa, abandonou ao mesmo tempo esferas de mesmo peso e verificou que elas chegavam ao solo no mesmo instante.
Quando dois corpos quaisquer são abandonados, no vácuo ou no ar com resistência desprezível, da mesma altura, o tempo de queda é o mesmo para ambos, mesmo que eles possuam pesos diferentes.
O movimento de queda livre trata-se de um movimento acelerado, sofre a ação da aceleração da gravidade, aceleração essa que é representada por g e é variável para cada ponto da superfície da Terra. Porém para o estudo de Física, e desprezando a resistência do ar, seu valor é constante e aproximadamente igual a 9,8 m/s2.
As equações matemáticas que determinam o movimento de queda livre são as seguintes:
O movimento de queda livre trata-se de um movimento acelerado, sofre a ação da aceleração da gravidade, aceleração essa que é representada por g e é variável para cada ponto da superfície da Terra. Porém para o estudo de Física, e desprezando a resistência do ar, seu valor é constante e aproximadamente igual a 9,8 m/s2.
As equações matemáticas que determinam o movimento de queda livre são as seguintes:
d é a distância percorrida pelo corpo até chegar ao chão;
G é a constante aceleração da gravidade;
t é o tempo que o corpo leva para chegar ao chão.
quarta-feira, 7 de outubro de 2015
Estudo do sinal da função afim
Estudando o sinal da função afim temos o seguinte entendimento . A função afim é representada pela equação do 1° grau . ax + b . Tendo em função crescente e decrescente, a>0 e a<0 . Temos x e y no gráfico, a raiz e os sinais . Agora vamos para a parte interessante o MACETÃO . Então temos CA_________MA , MA_____CA_____MA , __MA__ . ( Ma = mesmo que a, Ca = contrario de a )
EXEMPLOS :
Ca Ma
1 - sinal negativo em y e sinal positivo em x
2 - sinal positivo em y e sinal negativo em x
Isso na linha que é traçada passando pela raiz
Solução
F(x) = -6x + 30
F(x) = 0
-6x + 30 = 0
-6x = -30 .(-1)
6x = 30
X = 30/6
X = 5
Ca___ma
+ -
1 - F(x) > 0 quando x <5
2 - F(x) < 0 quando x > 5
3 - F(x) = 0 quando x = 5
EXEMPLOS :
Ca Ma
1 - sinal negativo em y e sinal positivo em x
2 - sinal positivo em y e sinal negativo em x
Isso na linha que é traçada passando pela raiz
Solução
F(x) = -6x + 30
F(x) = 0
-6x + 30 = 0
-6x = -30 .(-1)
6x = 30
X = 30/6
X = 5
Ca___ma
+ -
1 - F(x) > 0 quando x <5
2 - F(x) < 0 quando x > 5
3 - F(x) = 0 quando x = 5
terça-feira, 6 de outubro de 2015
Assinar:
Comentários (Atom)