Para justificar a definição de logaritmo, é necessário mostrar que a equação b^x = y tem a solução x e que esta é única, desde que y seja positivo e b seja positivo e diferente de 1. Uma prova para este fato requer o teorema do valor intermediário do cálculo elementar.Este teorema afirma que uma função contínua que produz dois valores m e n também produz qualquer valor que se situe entre m e n. Uma função é contínua quando ela não dá saltos, isto é, quando seu gráfico pode ser desenhado sem se levantar a caneta.
Pode-se demonstrar que esta propriedade se aplica à função f(x) = bx. Como f assume valores positivos arbitrariamente grandes e arbitrariamente pequenos, qualquer número y > 0 situa-se entre f(x 0) e f(x 1) para apropriados x 0 e x 1. Logo, o teorema do valor intermediário garante que a equação f(x) = y tem uma solução. Além disso, há apenas uma solução para essa equação, porque a função f é estritamente crescente (para b > 1) ou estritamente decrescente (para 0 < b < 1).
A única solução x é o logaritmo de y na base b, logb(y). A função que atribui a y o seu logaritmo é chamada de função logarítmica ou, simplesmente, logaritmo. A função log b(x) é essencialmente caracterizada pela fórmula do produto:
Exemplo:
log_b(xy) = log_b(x) + log_b(y).
Precisamente, o logaritmo em qualquer base b > 1 é a única função crescente f dos números reais para os reais que satisfaçam f(b) = 1 e f(xy)=f(x)+f(y).
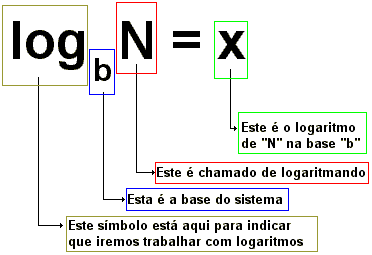
O logaritmo de um número é o expoente a que outro valor fixo, a base, deve ser elevado para produzir este número.
Exemplo:
O logaritmo de 1000 na base 10 é 3 porque 10 ao cubo é 1000
(1000 = 10 × 10 × 10 = 103).
De maneira geral, para quaisquer dois números reais b e x, onde b é positivo e b ≠ 1.
Nenhum comentário:
Postar um comentário